SEMANA
|
MES
|
TEMAS Y SUBTEMAS
|
|||||||||||||||||
15-20
|
FEBRERO
|
Repaso
|
|||||||||||||||||
22-27
|
FEBRERO
|
Repaso
|
|||||||||||||||||
29-5
|
FEBRERO/MARZO
|
Repaso
|
|||||||||||||||||
7-12
|
MARZO
|
Las
Funciones
|
|||||||||||||||||
14-19
|
MARZO
|
Sistema
de medidas de ángulos
|
|||||||||||||||||
22-26
|
MARZO
|
Definición
delas funciones en los triángulos
Funciones trigonométricas en el plano cartesiano
Las funciones trigonométricas en el plano cartesiano se describen como relaciones entre los lados de un triángulo rectángulo (triángulo en el cual uno de sus ángulos es recto).
Funciones trigonométricas en el plano cartesiano de ángulos agudos
Si el triángulo tiene un ángulo agudo θ se pueden encontrar seis razones entre las longitudes de los lados a,b y c del triángulo.
b/c, a/c, b/a, a/b, c/a, c/b
Estas relaciones dependen del ángulo θ y no del tamaño del triángulo. Si dos triángulos tienen ángulos iguales son semejantes y sus lados son proporcionales.
Las relaciones son funciones de θ y se les llama funciones trigonométricas. Las funciones trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante, sus símbolos respectivamente son: sen, cos, tan, cot, sec y csc.
Por ejemplo sen θ indica la relación b/c respecto a θ.
Si θ es el ángulo agudo del triángulo rectángulo entonces:
Sen θ = b/c
Cos θ = a/c
Tan θ = b/a
Cot θ = a/b
Sec θ = c/a
Csc θ = c/b
El dominio de cada una de las funciones trigonométricas es el conjunto de todos los ángulos agudos.
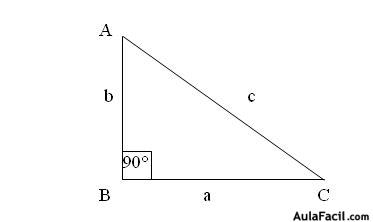
Si el ángulo θ es agudo a los lados del triángulo se les llama cateto adyacente, cateto opuesto e hipotenusa.
Es decir:
Sen θ = c. opuesto/hipotenusa
Cos θ = c. adyacente/hipotenusa
Tan θ = c. opuesto/c. adyacente
Cot θ = c. adyacente/c. opuesto
Sec θ = hipotenusa/c. adyacente
Csc θ = hipotenusa/c. opuesto
Los valores de las seis funciones trigonométricas son positivos para todo ángulo agudo θ.
Seno y cosecante son recíprocas entre sí.
Coseno y secante son recíprocas entre sí.
Tangente y cotangente son recíprocas entre sí.
Sen θ = 1/csc
Cos θ = 1/sec
Tan θ = 1/cot
Cot θ = 1/tan
Sec θ = 1/cos
Csc θ = 1/sen
EJEMPLO
Si el ángulo θ es agudo y cos θ = 3/5, calcula el valor de las seis funciones trigonométricas de θ.
Cateto adyacente = 3
Hipotenusa = 5
Aplicando el teorema de Pitágoras:
32 + (c. opuesto)2 = 52
(c. opuesto)2 = 52 – 32
(c. opuesto)2 = 16
Cateto opuesto = 4
Las funciones trigonométricas de este triángulo son las siguientes:
Sen θ = 4/5
Cos θ = 3/5
Tan θ = 4/3
Cot θ = 3/4
Sec θ = 5/3
Csc θ = 5/4
NOTA: Las calculadoras científicas tienen teclas como SIN, COS y TAN que se pueden usar para calcular los valores de esas funciones, antes de utilizar la calculadora para determinar los valores de funciones hay que seleccionar el modo grados o radián según nuestro ángulo.
Funciones trigonométricas en el plano cartesiano
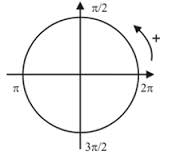
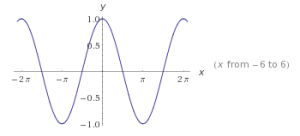
Al hacer las gráficas de las funciones trigonométricas siempre suponemos que los ángulos están en radianes.
EJEMPLO
Graficas de las siguientes funciones trigonométricas en el plano cartesiano
Y = sen t
Y = cos t
Y = tan t
Y = cot t
Y = sec t
y = csc t
|
|||||||||||||||||
28-2
|
MARZO-ABRIL
|
Ángulos
notables
 |
|||||||||||||||||
4-9
|
ABRIL
|
Empleo
de calculadora científica –evaluación
de funciones
|
|||||||||||||||||
11-16
|
ABRIL
|
Representación
grafica de las funciones
trigonométrica
Representación Gráfica de las Funciones Trigonométricas Representación gráfica de una función periódica
En la vida diaria existen muchos casos de funciones periódicas cuando la variable es el tiempo; situaciones como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es aquel en el que la posición(es) del sistema se pueden expresar en base a funciones periódicas, todas con el mismo período.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
Las funciones trigonométricas seno, coseno típicos de funciones periódicas, cuyo período es 360 grados. En el caso de la tangente, vemos que su periodo es menor, siendo 180 grados.
|
|||||||||||||||||
18-23
|
ABRIL
|
Resolución de triángulos rectángulos
3 Se conocen la hipotenusa y un ángulo agudo:
|
25-30
|
ABRIL
|
Problemas
de aplicación (Angulo de elevación y
depresión)
Ángulos de elevación y depresión
Frecuentemente resulta inconveniente o imposible medir distancias o ángulos directamente. Un ingeniero, un topógrafo, un astrónomo y un agrimensor, por ejemplo, cuando halla la altura de una colina o el curso exacto de un túnel en construcción, o la posición y la distancia entre dos estrellas, emplea ciertos instrumentos para medir indirectamente ángulos y distancias correspondientes a puntos inaccesibles, y luego aplica los principios básicos de trigonometría.
 Ejemplo: Ejemplo:h = ? d = 30 m o = 40° Para medir la altura h de un edificio, utilizamos las tablas trigonométricas o la calculadora científica y, la razón trigonométrica tan , esto es, tan = tan 40° = Luego, tan 40° = 0, 839099631… entonces, h = 30 tan 40° h = 25,17 m La altura del edificio es 25,17 m aproximadamente  Ejemplo: 
Un faro tiene una altura que mide 55 m. El ángulo de depresión desde la cima del faro hasta el barco en el mar es de 72°.
¿Qué tan lejos de la base del faro está el barco? Si x representa a la distancia, entonces: tan 72° = x = Luego, tan 72° = 3,077683537… por tanto, x = 17, 87 m * La distancia aproximada entre el barco y la base de la torre es de 17,87 m. Ejemplo:Una grúa que mide 2,5 m de alto; forma un ángulo de elevación de 21° con su palanca. El piso es horizontal. La grúa se encuentra a 100 m de la recta perpendicular a la palanca. Determinemos la medida de la altura desde el suelo hasta el punto más alto de la palanca. EJERCICIOS PROPUESTOSEjercicios: 1. El edificio más alto del mundo es la torre SEARS ubicada en la ciudad de Chicago, Illinois, E.U.A. Proyecta una sombra de 950 m cuándo el ángulo de elevación de los rayos solares es de 25°, ¿Cuál es la altura del edificio? 2. En la ciudad de Paris, Francia, se encuentra la torre Eiffel. En 1959 se instalo en lo alto de dicha torre una antena para radio y televisión de 20, 24 m de altura. Cuando el ángulo de elevación de los rayos solares es de 55°, la sombra proyectada por el conjunto es de 224, 61 m. ¿Cuál era la altura original de la torre Eiffel? 3. Determinar la medida de la altura de un edificio, sabiendo que cuando los rayos del sol forman un ángulo de depresión de 60° con dicho edificio, su sombra proyectada sobre el piso horizontal mide 60 m 4. El ángulo de elevación de un barco a la Cúspide de un faro de 50 m de alto, situado en la costa, mide 13°. ¿Qué tan lejos de la costa se encuentra el barco? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2-7
|
MAYO
|
Leyes
del Seno y Coseno
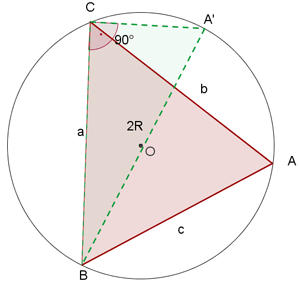
Teorema o ley del seno
Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
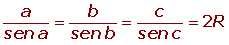  Ejercicios
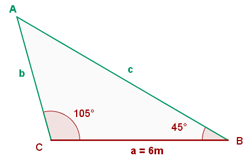
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Determina los restantes elementos.
 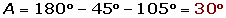 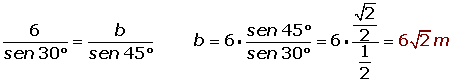 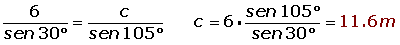
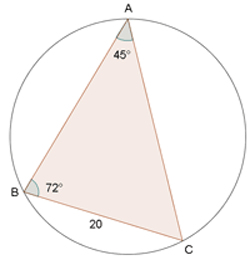
Hallar el radio del círculo circunscrito en un triángulo, donde A = 45°, B = 72° y a=20m.
 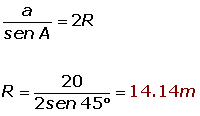 Teorema o ley del coseno
En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
 Ejemplos
Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.
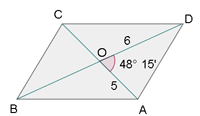  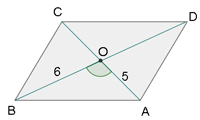 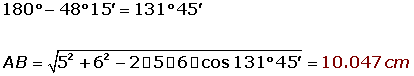
El radio de una circunferencia mide 25 m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud 36 m.
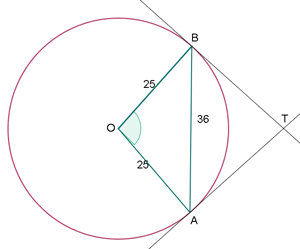 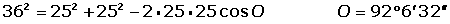  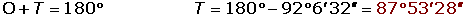 Teorema o ley de la tangente
Si A y B son ángulos de un triángulo y sus lados correspondientes son a y b, se cumple que:
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10-14
|
MAYO
|
Resolución
de triángulos oblicuángulos
Para resolver triángulos oblicuángulos vamos a utilizar los teoremas del seno y delcoseno.
Dependiendo de los elementos que conozcamos, nos encontramos con cuatro tipos deresolución de triángulos oblicuángulos:
1º. Conociendo un lado y dos ángulos adyacentes a él
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.
    2º. Conociendo dos lados y el ángulo comprendido
De un triángulo sabemos que: a = 10 m, b = 7 m y C = 30°. Calcula los restantes elementos.
     3º Conociendo dos lados y un ángulo opuesto
Supongamos que tenemos a, b y A; al aplicar el teorema de los senos puede suceder:
1. sen B > 1. No hay solución.
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 8 m.
 
Como el seno de un ángulo nunca puede ser mayor que 1, el problema no tiene solución. La figura muestra la imposibilidad de que exista el triángulo planteado.
2. sen B = 1. Solución única: triángulo rectángulo
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 6 m.
   3. sen B < 1. Una o dos soluciones
Resuelve el triángulo de datos: A = 60°, a = 8 m y b = 4 m.
    
Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 4 m.
       4º. Conociendo los tres lados
Resuelve el triángulo de datos: a = 15 m, b = 22 m y c = 17 m.
   |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
16-21
|
MAYO
|
Problemas
de aplicación
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
23-28
|
MAYO
|
Identidades
y Ecuaciones
Identidades TrigonométricasObjetivos
IntroducciónEn esta lección revisaremos las propiedades de las funciones trigonométricas que estudiamos anteriormente, desde el punto de vista algebraico. Utilizaremos estas propiedades para simplificar expresiones y para verificar identidades, ambas trigonométricas.Las identidades trigonométricas nos ayudan a simplificar expresiones complejas y de esta forma a comprender mejor el significado de la expresión. Identidades Trigonométricas Fundamentales
Simplificación de Expresiones TrigonométricasEjemplo 1:
Ejemplo 2:
Ejemplo 3:
Ejemplo 4:
Verificación de Identidades TrigonométricasVerificar una identidad trigonométrica consiste en demostrar que efectivamente ambos lados de la igualdad son equivalentes. Usaremos operaciones algebraicas e identidades trigonométricas conocidas para convertir uno de los lados de la ecuación exactamente en la forma en que está expresado el otro lado de la ecuación.Ejemplo 1:
Ejemplo 2:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
31-4
|
MAYO-JUNIO
|
Relaciones
Fundamentales deducción y demostración
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13-18
|
JUNIO
|
Demostración
de identidades
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
20-25
|
JUNIO
|
Solución
de Ecuaciones trigonometricas
Cómo resolver ecuaciones trigonométricas
Una ecuación trigonométrica es una ecuación que contiene una o varias funciones trigonométricas de la variable trigonométrica del arco x. Despejar “x” significa encontrar los valores de los arcos trigonométricos, cuyas funciones trigonométricas hacen que la ecuación trigonométrica sea correcta.
x = Pi/3; x = 5Pi/6; x = 3Pi/2; x = 45⁰; x = 37,12⁰; x = 178,37⁰
Pasos
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
27-2
|
JUNIO-JULIO
|
Geometría
Analitica
Coordenadas de un vector   Módulo   Vector unitario Suma  Resta Producto de un vector por un escalar Producto escalar de vectores Expresión analítica del producto escalar Expresión analítica del módulo de un vector Expresión analítica del ángulo de dos vectores Expresión analítica de la ortogonalidad de dos vectores ProyecciónCombinación lineal de vectoresSistema de referenciaDistancia entre dos puntos Coordenadas del punto medioSimétrico de un puntoDivisión de un segmentoPuntos alineadosCoordenadas del baricentroEcuaciones de la rectaVectorial Paramétricas Continua Pendiente   Punto-pendiente General  Explícita Canónica o segmentaria Que pasa por dos puntos Paralelas al eje OX Paralelas al eje OY Rectas paralelas   Rectas perpendiculares Posiciones relativasSecantes Paralelas Coincidentes Ángulo que forman dos rectas  Distancia de un punto a una recta Ecuaciones de las bisectrices Ecuación de la mediatriz CónicasEcuación de la circunferencia    Ecuación reducida Ecuación de la elipseExcentricidad Ecuación reducida De eje vertical De eje horizontal y centro distinto al origen  De eje vertical y centro distinto al origen Ecuación de la hipérbolaExcentricidad Asíntotas Ecuación reducida
F'(-c,0) y F(c,0)
 De eje vertical
F'(0, -c) y F(0, c)
 De eje horizontal y centro distinto al origen 
Donde A y B tienen signos opuestos.
De eje vertical y centro distinto al origen Hipérbola equilátera Asíntotas Excentricidad Referida a sus asíntotas Ecuación de la parábolaEcuación reducida de la parábolaDe ejes el de abscisas y de vértice (0, 0)    De ejes el de ordenadas y de vértice (0, 0)    Paralela a OX y vértice distinto al origen Paralela a OY, y vértice distinto al origen |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5-9
|
JULIO
|
Distancia
entre dos puntos
|
11-16
|
JULIO-
|
Ecuación
de la Recta
|
18
|
JULIO
|



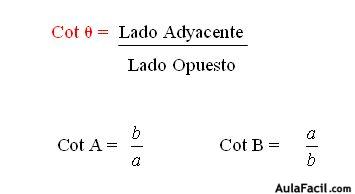




















































































No hay comentarios:
Publicar un comentario